Zihuan Qiu<br/>(邱子欢)

Zihuan Qiu
(邱子欢)

I am currently a second-year Ph.D. student at the School of Information and Communication Engineering, University of Electronic Science and Technology of China(UESTC, 电子科技大学) supervised by Prof. Fanman Meng (孟凡满).

My research primarily centers on continual learning and the efficient reuse of multimodal large language models and vision-language models. Earlier in my Ph.D. studies, I focused on class-incremental learning. More recently, I have become interested in model merging, exploring how the efficient integration of pre-trained models can enhance multi-task performance and support continual model adaptation.

🔥 News

  • 2025.09: 🎉 First-author paper accepted to NeurIPS 2025.
  • 2024.06: 🌍 Attended CVPR 2024 (Seattle, USA).
  • 2024.02: 🎉 First-author paper accepted to CVPR 2024.
  • 2022.12: 🎉 First-author paper accepted to Neurocomputing 2023.
  • 2021.10: 🎉 First-author paper accepted to SPIE Medical Imaging 2022.

📝 Selected Publications

NeurIPS 2025
sym

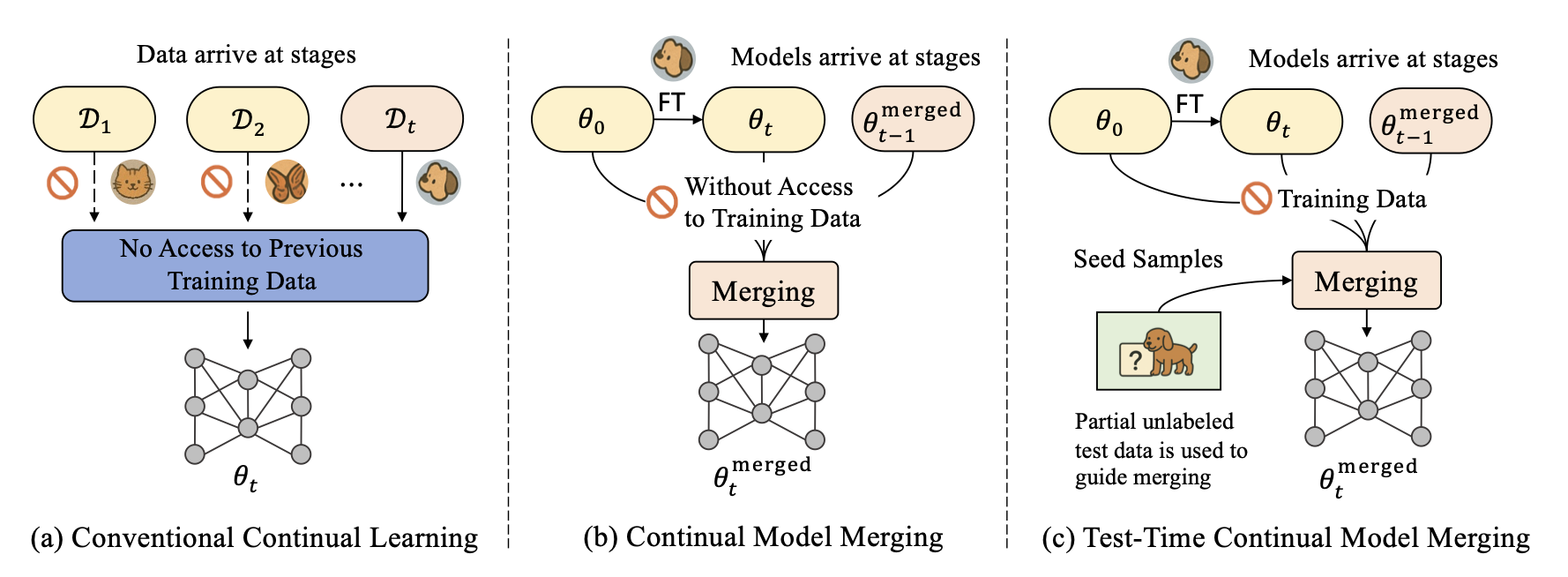
MINGLE: Mixtures of Null-Space Gated Low-Rank Experts for Test-Time Continual Model Merging
Zihuan Qiu, Yi Xu, Chiyuan He, Fanman Meng, Linfeng Xu, Qingbo Wu, Hongliang Li

  • TTCMM: Formalizes Test-Time Continual Model Merging.
  • MINGLE: Adaptive null-space gated low-rank experts, balancing stability and plasticity.
CVPR 2024
sym

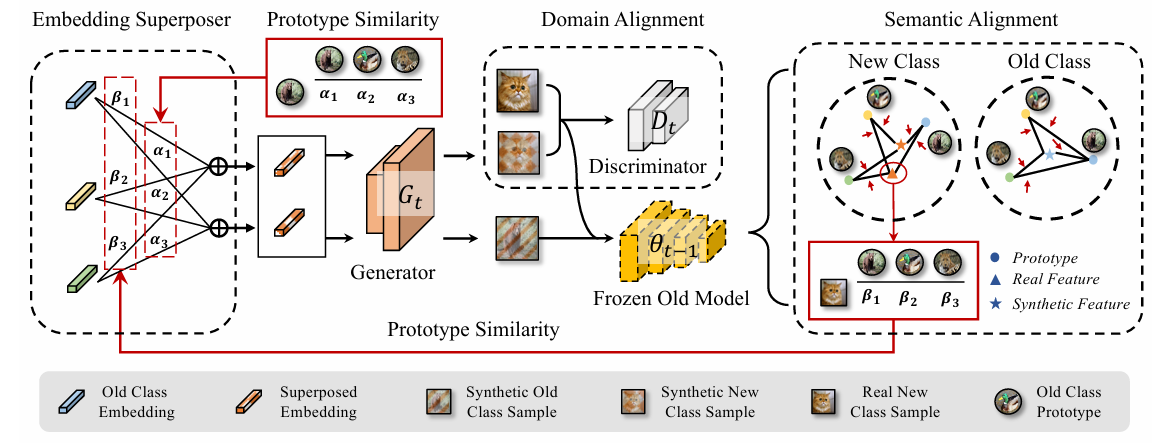
Dual-consistency Model Inversion for Non-exemplar Class Incremental Learning
Zihuan Qiu, Yi Xu, Fanman Meng, Hongliang Li, Linfeng Xu, Qingbo Wu

  • DCMI: Semantic + domain consistency for high-fidelity synthetic replay.
  • Prototypical Routing: Reduces bias, boosts old-class accuracy.
Neurocomputing 2023
sym

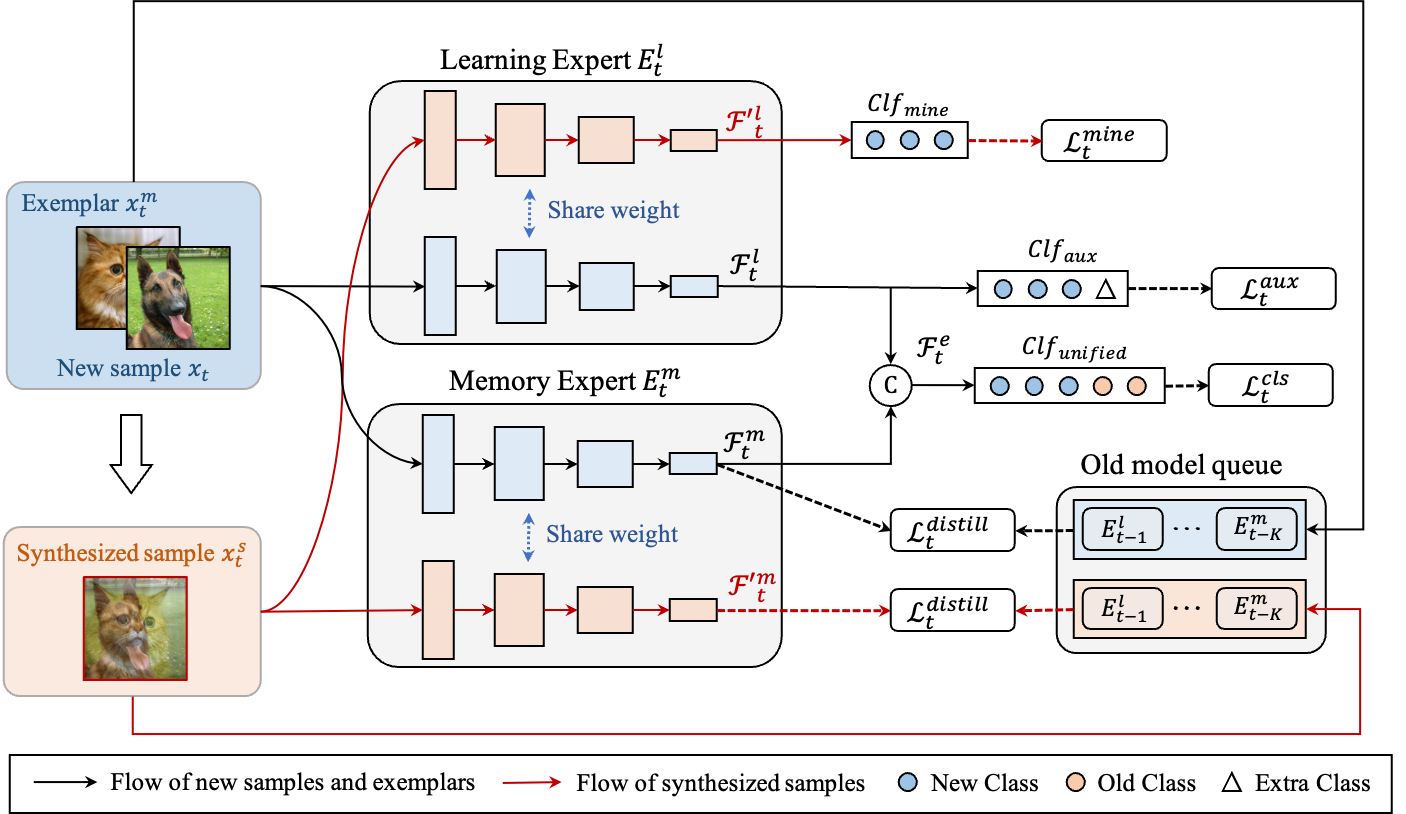
ISM-Net: Mining incremental semantics for class incremental learning
Zihuan Qiu, Linfeng Xu, Zhichuan Wang, Qingbo Wu, Fanman Meng, Hongliang Li

  • ISM: Strips old-class semantics from new features to reduce confusion.
  • Lightweight Expansion + Old-Model Queue: Preserves early knowledge with minimal memory.

Preprints

Arxiv
sym

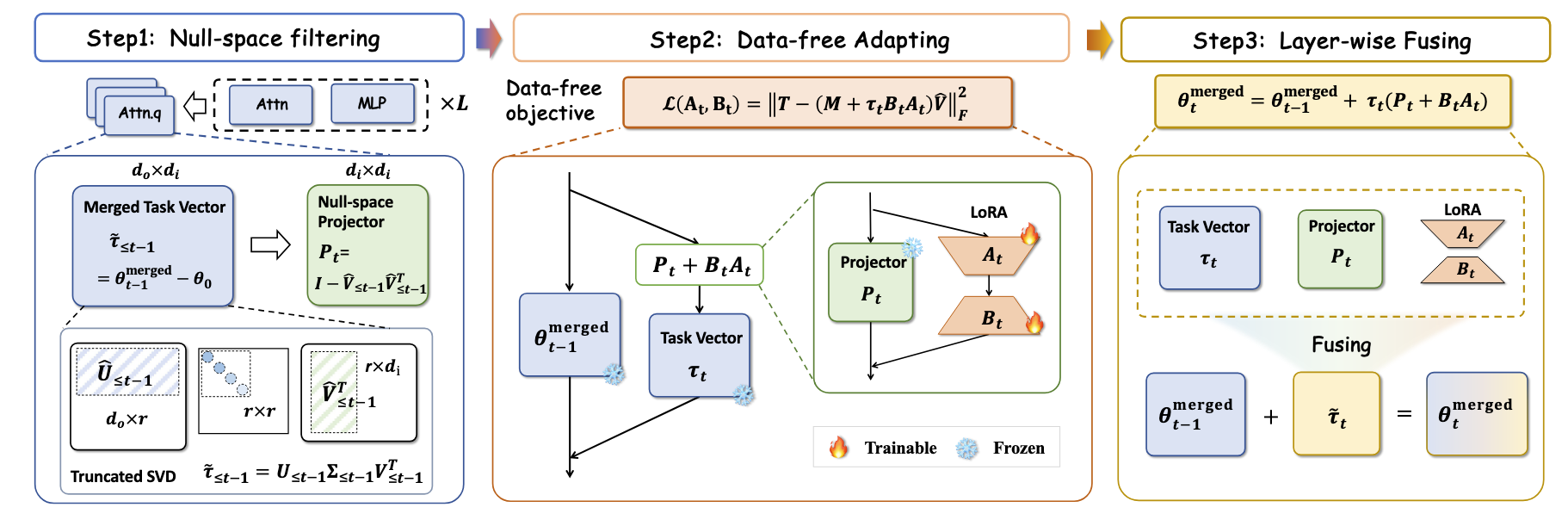
Null-Space Filtering for Data-Free Continual Model Merging: Preserving Transparency, Promoting Fidelity
Zihuan Qiu, Lei Wang, Yang Cao, Runtong Zhang, Bing Su, Yi Xu, Fanman Meng, Linfeng Xu, Qingbo Wu, Hongliang Li

  • Challenge: Transparency and fidelity as fundamental desiderata in data-free model merging.
  • NUFILT: Combines null-space filtering with projection-aware adaptation.
Arxiv
sym

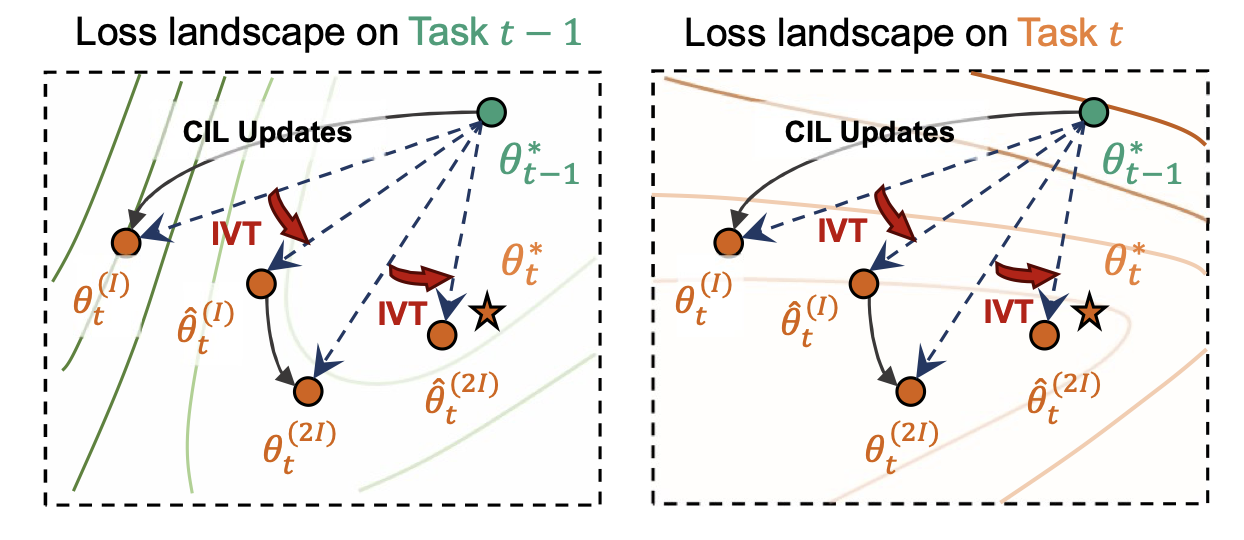
Closing the Oracle Gap: Increment Vector Transformation for Class Incremental Learning
Zihuan Qiu, Yi Xu, Fanman Meng, Runtong Zhang, Linfeng Xu, Qingbo Wu, Hongliang Li

  • LMC in CIL Oracles: Reveal favorable linear mode connectivity and identify mismatch between naive updates and oracle solutions.
  • IVT: Curvature-guided transformation using Fisher approximation, boosting accuracy and reducing forgetting across CIL settings.

Other Publications

  • TMM 2025 [DesCLIP: Robust Continual Adaptation via General Attribute Descriptions for Pretrained Vision-Language Models], Chiyuan He, Zihuan Qiu, Fanman Meng, Linfeng Xu, Qingbo Wu, Hongliang Li.
  • ICIP 2025 [DPM-CLIP: Zero-Shot Multimodal Egocentric Activity Recognition based on Dual-Prediction Mechanism], Yukun Chen, Liang Wan, Zihuan Qiu, Mingzhou He, Fanman Meng, Linfeng Xu, Qingbo Wu, Hongliang Li.
  • TMM 2025 [Distribution-Level Memory Recall for Continual Learning: Preserving Knowledge and Avoiding Confusion], Shaoxu Cheng, Kanglei Geng, Chiyuan He, Zihuan Qiu, Linfeng Xu, Heqian Qiu, Lanxiao Wang, Qingbo Wu, Fanman Meng, Hongliang Li.
  • ICASSP 2025 [Leveraging Pre-Trained Models for Multimodal Class-Incremental Learning under Adaptive Fusion], Yukun Chen, Zihuan Qiu, Fanman Meng, Hongliang Li, Linfeng Xu, Qingbo Wu.
  • IEEE Sensors Journal 2024 [Continual Egocentric Activity Recognition with Foreseeable-Generalized Visual-IMU Representations], Chiyuan He, Shaoxu Cheng, Zihuan Qiu, Linfeng Xu, Fanman Meng, Qingbo Wu, Hongliang Li.
  • Neurocomputing 2023 [GFR: Generic feature representations for class incremental learning], Zhichuan Wang, Linfeng Xu, Zihuan Qiu, Qingbo Wu, Fanman Meng, Hongliang Li.
  • ICASSP 2023 [MFAT: A multi-level feature aggregated transformer for person re-identification],Bowen Tan, Linfeng Xu, Zihuan Qiu, Qingbo Wu, Fanman Meng.
  • ICIP 2022 [Eldnet: Establishment and refinement of edge likelihood distributions for camouflaged object detection], Chiyuan He, Linfeng Xu, Zihuan Qiu.
  • SPIE Medical Imaging 2022 BDG-Net: boundary distribution guided network for accurate polyp segmentation, Zihuan Qiu, Zhichuan Wang, Miaomiao Zhang, Ziyong Xu, Jie Fan, Linfeng Xu.

🎓 Educations

  • Ph.D. Student, Information and Communication Engineering
    University of Electronic Science and Technology of China (UESTC), Chengdu
    2023.09 – Present

  • M.S. Student, Electronic Information
    University of Electronic Science and Technology of China (UESTC), Chengdu
    2020.09 – 2023.06

  • B.Eng., Communication Engineering
    Tiangong University, Tianjin
    2015.09 – 2019.06

🛠️ Services

Reviewer for: NeurIPS 2025 · ICLR 2025 · MM 2025 · ICME 2025 · ICASSP 2025

💻 Internships

  • Research Intern, JIIGAN / MEGVII, Chengdu
    2025.09 – Present