权值初始化

发表于 更新于 分类于

1. 梯度消失与爆炸

对于一个没有激活函数（先不考虑激活函数）的多层神经网络，参数的导数可以计算如下

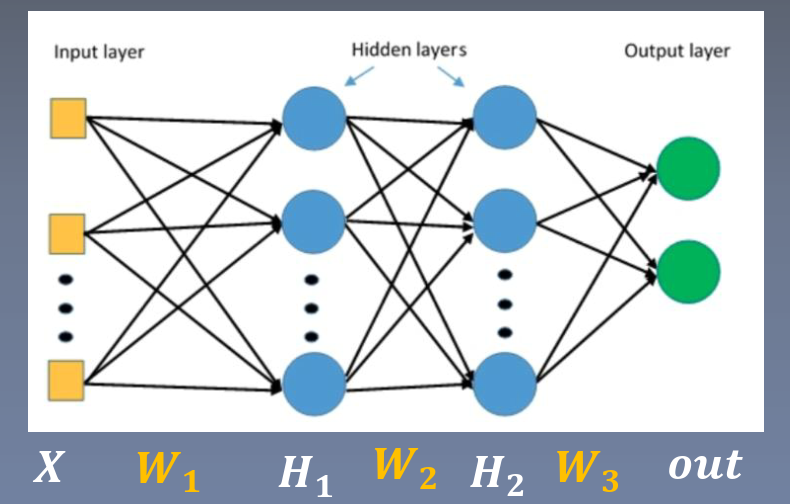
image-20200801210729523

H2=H1∗W2ΔW2=∂Loss∂W2=∂Loss∂out∗∂out∂H2∗∂H2∂w2=∂Loss∂out∗∂out∂H2∗H1\begin{aligned} \text{H}_2&=\text{H}_1*\text{W}_2 \\ \Delta \text{W}_2&=\frac{\partial \text{Loss}}{\partial \text{W}_2}=\frac{\partial \text{Loss}}{\partial \text{out}}*\frac{\partial \text{out}}{\partial \text{H}_2}*\frac{\partial \text{H}_2}{\partial \text{w}_2}\\ &=\frac{\partial \text{Loss}}{\partial \text{out}}*\frac{\partial \text{out}}{\partial \text{H}_2}*\text{H}_1\\ \end{aligned}

因此参数的导数与隐藏层H1的输出值有关：

梯度消失：H1→0⇒ΔW2→0\mathrm{H}_{1} \rightarrow \mathbf{0} \Rightarrow \Delta \mathrm{W}_{2} \rightarrow \mathbf{0}

梯度爆炸：H1→∞⇒ΔW2→∞\mathrm{H}_{1} \rightarrow \infty \Rightarrow \Delta \mathrm{W}_{2} \rightarrow \infty

实验代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import os
import torch
import random
import numpy as np
import torch.nn as nn
from tools.common_tools import set_seed

set_seed(1)  # 设置随机种子


class MLP(nn.Module):
    def __init__(self, neural_num, layers):
        super(MLP, self).__init__()
        self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
        self.neural_num = neural_num

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
        return x

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
				nn.init.normal_(m.weight.data)  # normal: mean=0, std=1
                
                
layer_nums = 100
neural_nums = 256
batch_size = 16

net = MLP(neural_nums, layer_nums)
net.initialize()

inputs = torch.randn((batch_size, neural_nums))  # normal: mean=0, std=1

output = net(inputs)
print(output)

这里我们构造了一个100层，每一层有256个神经元的全连接线性网络，参数初始化用的是标准正态分布的方法。在随机生成了一个batch_size=16的，满足标准正态分布的输入，观察模型输出。

1
2
3
4
5
6
7
tensor([[nan, nan, nan,  ..., nan, nan, nan],
        [nan, nan, nan,  ..., nan, nan, nan],
        [nan, nan, nan,  ..., nan, nan, nan],
        ...,
        [nan, nan, nan,  ..., nan, nan, nan],
        [nan, nan, nan,  ..., nan, nan, nan],
        [nan, nan, nan,  ..., nan, nan, nan]], grad_fn=<MmBackward>)

发现输出变成了nan（过大或者过小，超出当前精度范围）。我们改一下代码，判断在前向传播中什么时候参数变成了nan（观察每一层参数的标准差）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import os
import torch
import random
import numpy as np
import torch.nn as nn
from tools.common_tools import set_seed

set_seed(1)  # 设置随机种子

class MLP(nn.Module):
    def __init__(self, neural_num, layers):
        super(MLP, self).__init__()
        self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
        self.neural_num = neural_num

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
            print("layer:{}, std:{}".format(i, x.std()))
            if torch.isnan(x.std()):
                print("output is nan in {} layers".format(i))
                break
        return x

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
				nn.init.normal_(m.weight.data)  # normal: mean=0, std=1

代码运行结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
layer:0, std:15.959932327270508
layer:1, std:256.6237487792969
layer:2, std:4107.24560546875
layer:3, std:65576.8125
layer:4, std:1045011.875
layer:5, std:17110408.0
layer:6, std:275461408.0
layer:7, std:4402537984.0
layer:8, std:71323615232.0
layer:9, std:1148104736768.0
layer:10, std:17911758454784.0
layer:11, std:283574846619648.0
layer:12, std:4480599809064960.0
layer:13, std:7.196814275405414e+16
layer:14, std:1.1507761512626258e+18
layer:15, std:1.853110740188555e+19
layer:16, std:2.9677725826641455e+20
layer:17, std:4.780376223769898e+21
layer:18, std:7.613223480799065e+22
layer:19, std:1.2092652108825478e+24
layer:20, std:1.923257075956356e+25
layer:21, std:3.134467063655912e+26
layer:22, std:5.014437766285408e+27
layer:23, std:8.066615144249704e+28
layer:24, std:1.2392661553516338e+30
layer:25, std:1.9455688099759845e+31
layer:26, std:3.0238180658999113e+32
layer:27, std:4.950357571077011e+33
layer:28, std:8.150925520353362e+34
layer:29, std:1.322983152787379e+36
layer:30, std:2.0786820453988485e+37
layer:31, std:nan
output is nan in 31 layers
tensor([[        inf, -2.6817e+38,         inf,  ...,         inf,
                 inf,         inf],
        [       -inf,        -inf,  1.4387e+38,  ..., -1.3409e+38,
         -1.9659e+38,        -inf],
        [-1.5873e+37,         inf,        -inf,  ...,         inf,
                -inf,  1.1484e+38],
        ...,
        [ 2.7754e+38, -1.6783e+38, -1.5531e+38,  ...,         inf,
         -9.9440e+37, -2.5132e+38],
        [-7.7184e+37,        -inf,         inf,  ..., -2.6505e+38,
                 inf,         inf],
        [        inf,         inf,        -inf,  ...,        -inf,
                 inf,  1.7432e+38]], grad_fn=<MmBackward>)

我们发现第31层的参数的标准差变成了无穷。每一层的标准差都在逐渐变大，直到第31层达到了nan。

我们来研究一下，为什么用标准正态分布设置的输入和参数会在前向传播过程中逐渐变大，最终爆炸。

下面是一些数学基础：

若X\boldsymbol{X}与Y\boldsymbol{Y}独立，则有以下结论：

  1. E(X∗Y)=E(X)∗E(Y)\mathrm{E}(\boldsymbol{X} * \boldsymbol{Y})=\boldsymbol{E}(\boldsymbol{X}) * \boldsymbol{E}(\boldsymbol{Y})

  2. D(X)=E(X2)−[E(X)]2\mathrm{D}(\boldsymbol{X})=\boldsymbol{E}\left(\mathrm{X}^{2}\right)-[\boldsymbol{E}(\boldsymbol{X})]^{2}

  3. D(X+Y)=D(X)+D(Y)\mathrm{D}(\boldsymbol{X}+\boldsymbol{Y})=\boldsymbol{D}(\boldsymbol{X})+\boldsymbol{D}(\boldsymbol{Y})

  4. D(X∗Y)=D(X)∗D(Y)+D(X)∗[E(Y)]2+D(Y)∗[E(X)]2\mathrm{D}(\mathrm{X} * \mathrm{Y})=\mathrm{D}(\mathrm{X}) * \mathrm{D}(\mathrm{Y})+\mathrm{D}(\mathrm{X}) *[E(\boldsymbol{Y})]^{2}+\mathrm{D}(\mathrm{Y}) *[E(X)]^{2}

    若 E(X)=0,E(Y)=0\mathrm{E}(\mathrm{X})=0, \mathrm{E}(\mathrm{Y})=0，则D(X∗Y)=D(X)∗D(Y)\mathrm{D}(\mathrm{X} * \mathrm{Y})=\mathrm{D}(\mathrm{X}) * \mathrm{D}(\mathrm{Y})

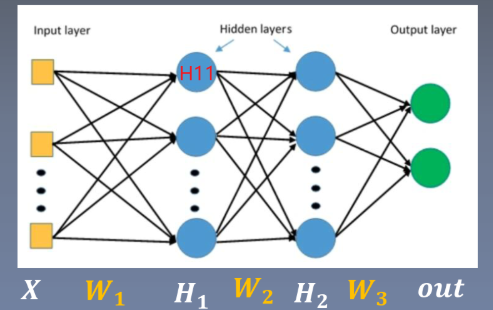
image-20200801214436134

H11=∑i=0nXi∗W1i\mathrm{H}_{11}=\sum_{i=0}^{n} X_{i} * W_{1 i}

D(H11)=∑i=0nD(Xi)∗D(W1i)=n∗(1∗1)=n\begin{aligned} \mathbf{D}\left(\mathrm{H}_{11}\right) &=\sum_{i=0}^{n} \boldsymbol{D}\left(\boldsymbol{X}_{i}\right) * \boldsymbol{D}\left(\boldsymbol{W}_{1 i}\right) \\ &=\mathrm{n} *(1 * 1) \\ &=\mathrm{n} \end{aligned}

X和W都是零均值，标准差为1的标准正态分布，且X和W相互独立。

std⁡(H11)=D(H11)=n\operatorname{std}\left(\mathrm{H}_{11}\right)=\sqrt{\mathbf{D}\left(\mathrm{H}_{11}\right)}=\sqrt{n}

于是，我们就发现了每经过一层传播，数据的标准差就扩大n\sqrt{n}倍，也就是数据之间开始扩散。上面我们的实验中，n=256，从各层参数的标准差打印信息来看，确实是每一层的标准差扩大15倍的关系。

为了防止各层的标准差在前向传播的过程中逐渐变大，一个好的方法是将每一层的参数的标准差设为1/n，则每一层输出的标准差都能位置在1附近，解决了参数爆炸的问题。

D(W)=1n⇒std⁡(W)=1nD(W)=\frac{1}{n} \Rightarrow \operatorname{std}(W)=\sqrt{\frac{1}{n}}

我们重新改一下代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import os
import torch
import random
import numpy as np
import torch.nn as nn
from tools.common_tools import set_seed

set_seed(1)  # 设置随机种子

class MLP(nn.Module):
    def __init__(self, neural_num, layers):
        super(MLP, self).__init__()
        self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
        self.neural_num = neural_num

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
            print("layer:{}, std:{}".format(i, x.std()))
            if torch.isnan(x.std()):
                print("output is nan in {} layers".format(i))
                break
        return x

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
				nn.init.normal_(m.weight.data, std=np.sqrt(1/self.neural_num))

运行结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
layer:0, std:0.9974957704544067
layer:1, std:1.0024365186691284
layer:2, std:1.002745509147644
layer:3, std:1.0006227493286133
layer:4, std:0.9966009855270386
layer:5, std:1.019859790802002
layer:6, std:1.026173710823059
layer:7, std:1.0250457525253296
layer:8, std:1.0378952026367188
layer:9, std:1.0441951751708984
layer:10, std:1.0181655883789062
layer:11, std:1.0074602365493774
layer:12, std:0.9948930144309998
layer:13, std:0.9987586140632629
layer:14, std:0.9981392025947571
layer:15, std:1.0045733451843262
layer:16, std:1.0055204629898071
layer:17, std:1.0122840404510498
layer:18, std:1.0076017379760742
layer:19, std:1.000280737876892
layer:20, std:0.9943006038665771
layer:21, std:1.012800931930542
layer:22, std:1.012657642364502
layer:23, std:1.018149971961975
layer:24, std:0.9776086211204529
layer:25, std:0.9592394828796387
layer:26, std:0.9317858815193176
layer:27, std:0.9534041881561279
layer:28, std:0.9811319708824158
layer:29, std:0.9953019022941589
layer:30, std:0.9773916006088257
layer:31, std:0.9655940532684326
layer:32, std:0.9270440936088562
layer:33, std:0.9329946637153625
layer:34, std:0.9311841726303101
layer:35, std:0.9354336261749268
layer:36, std:0.9492132067680359
layer:37, std:0.9679954648017883
layer:38, std:0.9849981665611267
layer:39, std:0.9982335567474365
layer:40, std:0.9616852402687073
layer:41, std:0.9439758658409119
layer:42, std:0.9631161093711853
layer:43, std:0.958673894405365
layer:44, std:0.9675614237785339
layer:45, std:0.9837557077407837
layer:46, std:0.9867278337478638
layer:47, std:0.9920817017555237
layer:48, std:0.9650403261184692
layer:49, std:0.9991624355316162
layer:50, std:0.9946174025535583
layer:51, std:0.9662044048309326
layer:52, std:0.9827387928962708
layer:53, std:0.9887880086898804
layer:54, std:0.9932605624198914
layer:55, std:1.0237400531768799
layer:56, std:0.9702046513557434
layer:57, std:1.0045380592346191
layer:58, std:0.9943899512290955
layer:59, std:0.9900636076927185
layer:60, std:0.99446702003479
layer:61, std:0.9768352508544922
layer:62, std:0.9797843098640442
layer:63, std:0.9951220750808716
layer:64, std:0.9980446696281433
layer:65, std:1.0086933374404907
layer:66, std:1.0276142358779907
layer:67, std:1.0429234504699707
layer:68, std:1.0197855234146118
layer:69, std:1.0319130420684814
layer:70, std:1.0540012121200562
layer:71, std:1.026781439781189
layer:72, std:1.0331352949142456
layer:73, std:1.0666675567626953
layer:74, std:1.0413838624954224
layer:75, std:1.0733673572540283
layer:76, std:1.0404183864593506
layer:77, std:1.0344083309173584
layer:78, std:1.0022705793380737
layer:79, std:0.99835205078125
layer:80, std:0.9732587337493896
layer:81, std:0.9777462482452393
layer:82, std:0.9753198623657227
layer:83, std:0.9938382506370544
layer:84, std:0.9472599029541016
layer:85, std:0.9511011242866516
layer:86, std:0.9737769961357117
layer:87, std:1.005651831626892
layer:88, std:1.0043526887893677
layer:89, std:0.9889539480209351
layer:90, std:1.0130352973937988
layer:91, std:1.0030947923660278
layer:92, std:0.9993206262588501
layer:93, std:1.0342745780944824
layer:94, std:1.031973123550415
layer:95, std:1.0413124561309814
layer:96, std:1.0817031860351562
layer:97, std:1.128799557685852
layer:98, std:1.1617802381515503
layer:99, std:1.2215303182601929
tensor([[-1.0696, -1.1373,  0.5047,  ..., -0.4766,  1.5904, -0.1076],
        [ 0.4572,  1.6211,  1.9659,  ..., -0.3558, -1.1235,  0.0979],
        [ 0.3908, -0.9998, -0.8680,  ..., -2.4161,  0.5035,  0.2814],
        ...,
        [ 0.1876,  0.7971, -0.5918,  ...,  0.5395, -0.8932,  0.1211],
        [-0.0102, -1.5027, -2.6860,  ...,  0.6954, -0.1858, -0.8027],
        [-0.5871, -1.3739, -2.9027,  ...,  1.6734,  0.5094, -0.9986]],
       grad_fn=<MmBackward>)

我们看到，已经解决了参数爆炸的问题。我们以上实现都是基于没有激活函数的情况考虑的，现在我们加上激活函数（选择为tanh），再观察输出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import os
import torch
import random
import numpy as np
import torch.nn as nn
from tools.common_tools import set_seed

set_seed(1)  # 设置随机种子

class MLP(nn.Module):
    def __init__(self, neural_num, layers):
        super(MLP, self).__init__()
        self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
        self.neural_num = neural_num

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
            x = torch.tanh(x)
            print("layer:{}, std:{}".format(i, x.std()))
            if torch.isnan(x.std()):
                print("output is nan in {} layers".format(i))
                break
        return x

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
				nn.init.normal_(m.weight.data, std=np.sqrt(1/self.neural_num))

运行结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
layer:0, std:0.6273701786994934
layer:1, std:0.48910173773765564
layer:2, std:0.4099564850330353
layer:3, std:0.35637012124061584
layer:4, std:0.32117360830307007
layer:5, std:0.2981105148792267
layer:6, std:0.27730831503868103
layer:7, std:0.2589356303215027
layer:8, std:0.2468511462211609
layer:9, std:0.23721906542778015
layer:10, std:0.22171513736248016
layer:11, std:0.21079954504966736
layer:12, std:0.19820132851600647
layer:13, std:0.19069305062294006
layer:14, std:0.18555502593517303
layer:15, std:0.17953835427761078
layer:16, std:0.17485804855823517
layer:17, std:0.1702701896429062
layer:18, std:0.16508983075618744
layer:19, std:0.1591130942106247
layer:20, std:0.15480302274227142
layer:21, std:0.15263864398002625
layer:22, std:0.148549422621727
layer:23, std:0.14617665112018585
layer:24, std:0.13876433670520782
layer:25, std:0.13316625356674194
layer:26, std:0.12660598754882812
layer:27, std:0.12537944316864014
layer:28, std:0.12535445392131805
layer:29, std:0.1258980631828308
layer:30, std:0.11994212120771408
layer:31, std:0.11700888723134995
layer:32, std:0.11137298494577408
layer:33, std:0.11154613643884659
layer:34, std:0.10991233587265015
layer:35, std:0.10996390879154205
layer:36, std:0.10969001054763794
layer:37, std:0.10975217074155807
layer:38, std:0.11063199490308762
layer:39, std:0.11021336913108826
layer:40, std:0.10465587675571442
layer:41, std:0.10141163319349289
layer:42, std:0.1026025339961052
layer:43, std:0.10079070925712585
layer:44, std:0.10096712410449982
layer:45, std:0.10117629915475845
layer:46, std:0.10145658254623413
layer:47, std:0.09987485408782959
layer:48, std:0.09677786380052567
layer:49, std:0.099615179002285
layer:50, std:0.09867013245820999
layer:51, std:0.09398546814918518
layer:52, std:0.09388342499732971
layer:53, std:0.09352942556142807
layer:54, std:0.09336657077074051
layer:55, std:0.094817616045475
layer:56, std:0.08856320381164551
layer:57, std:0.09024856984615326
layer:58, std:0.0886448472738266
layer:59, std:0.08766943961381912
layer:60, std:0.08726290613412857
layer:61, std:0.08623497188091278
layer:62, std:0.08549781143665314
layer:63, std:0.08555219322443008
layer:64, std:0.08536665141582489
layer:65, std:0.08462796360254288
layer:66, std:0.08521939814090729
layer:67, std:0.08562128990888596
layer:68, std:0.08368432521820068
layer:69, std:0.08476376533508301
layer:70, std:0.08536301553249359
layer:71, std:0.08237562328577042
layer:72, std:0.08133520931005478
layer:73, std:0.08416961133480072
layer:74, std:0.08226993680000305
layer:75, std:0.08379077166318893
layer:76, std:0.08003699779510498
layer:77, std:0.07888863980770111
layer:78, std:0.07618381083011627
layer:79, std:0.07458438724279404
layer:80, std:0.07207277417182922
layer:81, std:0.07079191505908966
layer:82, std:0.0712786540389061
layer:83, std:0.07165778428316116
layer:84, std:0.06893911212682724
layer:85, std:0.06902473419904709
layer:86, std:0.07030880451202393
layer:87, std:0.07283663004636765
layer:88, std:0.07280216366052628
layer:89, std:0.07130247354507446
layer:90, std:0.07225216180086136
layer:91, std:0.0712454691529274
layer:92, std:0.07088855654001236
layer:93, std:0.0730612725019455
layer:94, std:0.07276969403028488
layer:95, std:0.07259569317102432
layer:96, std:0.0758652538061142
layer:97, std:0.07769152522087097
layer:98, std:0.07842093706130981
layer:99, std:0.08206242322921753
tensor([[-0.1103, -0.0739,  0.1278,  ..., -0.0508,  0.1544, -0.0107],
        [ 0.0807,  0.1208,  0.0030,  ..., -0.0385, -0.1887, -0.0294],
        [ 0.0321, -0.0833, -0.1482,  ..., -0.1133,  0.0206,  0.0155],
        ...,
        [ 0.0108,  0.0560, -0.1099,  ...,  0.0459, -0.0961, -0.0124],
        [ 0.0398, -0.0874, -0.2312,  ...,  0.0294, -0.0562, -0.0556],
        [-0.0234, -0.0297, -0.1155,  ...,  0.1143,  0.0083, -0.0675]],
       grad_fn=<TanhBackward>)

可以发现，添加了激活函数以后，每一层数据的标准差逐渐减小，这是我们不希望看到的。

2. Xavier方法与Kaiming方法

2.1 Xavier方法

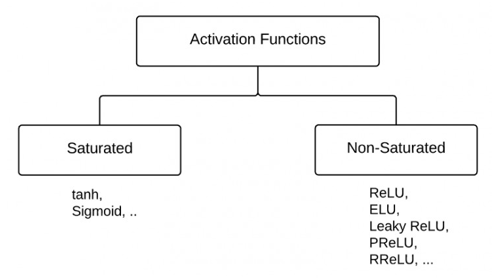
在论文[1]中，提出了一种参数初始化的方法，适用于饱和激活函数，如Sigmoid，Tanh

D(W)=2ni+ni+1\boldsymbol{D}(\boldsymbol{W})=\frac{2}{\boldsymbol{n}_{i}+\boldsymbol{n}_{i+1}}

nin_i是第ii层的神经元个数，ni+1n_{i+1}是第i+1i+1层的神经元个数

并且W∼U[−a,a]W \sim U[-a, a]，即WW是服从对称均匀分布的，可以反解出aa的值，得到：

W∼U[−6ni+ni+1,6ni+ni+1]W \sim U\left[-\frac{\sqrt{6}}{\sqrt{n_{i}+n_{i+1}}}, \frac{\sqrt{6}}{\sqrt{n_{i}+n_{i+1}}}\right]

其实可以发现，当ni=ni+1\boldsymbol{n}_{i}=\boldsymbol{n}_{i+1}时，和上面的方法是一样的，Xavier方法只是考虑了前后层神经元不等的情况，取了一个平均值。

另外，加上激活函数后，由于数据在通过激活函数之前和通过激活函数之后的标准差会有变化：

1
2
3
4
5
x = torch.randn(10000)
out = torch.tanh(x)

gain = x.std() / out.std()
print('gain:{}'.format(gain))
1
gain:1.5982500314712524

通过实验，可以发现tanh输入和输出标准差的比值是gain = 1.6左右，即输出比输入应该是1/gain。

所以说，经过激活函数，数据的标准差会被乘上一个增益(1/gain)，这个增益会造成数据标准差一致性被破坏，因此在初始化参数时，应该把激活函数的影响考虑进去。

在考虑了激活函数之后，参数的分布应该为：

D(W)=2gain2(ni+ni+1)\boldsymbol{D}\left( \boldsymbol{W} \right) =\frac{2gain^2}{\left( \boldsymbol{n}_i+\boldsymbol{n}_{i+1} \right)}，则W∼U[−gain⋅6ni+ni+1  ,gain⋅6ni+ni+1]W\sim U\left[ -gain\cdot \frac{\sqrt{6}}{\sqrt{n_i+n_{i+1}}}\,\, , gain\cdot \frac{\sqrt{6}}{\sqrt{n_i+n_{i+1}}} \right]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import os
import torch
import random
import numpy as np
import torch.nn as nn
from tools.common_tools import set_seed

set_seed(1)  # 设置随机种子

class MLP(nn.Module):
    def __init__(self, neural_num, layers):
        super(MLP, self).__init__()
        self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
        self.neural_num = neural_num

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
            x = torch.tanh(x)
            print("layer:{}, std:{}".format(i, x.std()))
            if torch.isnan(x.std()):
                print("output is nan in {} layers".format(i))
                break
        return x

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                a = np.sqrt(6 / (self.neural_num + self.neural_num))
                
                a *= 1.6								
                
                nn.init.uniform_(m.weight.data, -a, a)

输出结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
layer:0, std:0.7478928565979004
layer:1, std:0.6779849529266357
layer:2, std:0.6506703495979309
layer:3, std:0.6364355087280273
layer:4, std:0.6358171701431274
layer:5, std:0.6329374313354492
layer:6, std:0.6291818022727966
layer:7, std:0.6261899471282959
layer:8, std:0.6248595118522644
layer:9, std:0.6203226447105408
layer:10, std:0.6218484044075012
layer:11, std:0.6311259865760803
layer:12, std:0.6389117240905762
layer:13, std:0.6308977603912354
layer:14, std:0.6316721439361572
layer:15, std:0.6307259202003479
layer:16, std:0.6327394247055054
layer:17, std:0.6350437998771667
layer:18, std:0.6291753053665161
layer:19, std:0.6264926195144653
layer:20, std:0.6255913972854614
layer:21, std:0.6265914440155029
layer:22, std:0.629246711730957
layer:23, std:0.6324419379234314
layer:24, std:0.63409423828125
layer:25, std:0.625957190990448
layer:26, std:0.6308732628822327
layer:27, std:0.6323292255401611
layer:28, std:0.631292998790741
layer:29, std:0.6316223740577698
layer:30, std:0.6341015100479126
layer:31, std:0.6347006559371948
layer:32, std:0.6258944869041443
layer:33, std:0.6284964084625244
layer:34, std:0.6349349617958069
layer:35, std:0.6348815560340881
layer:36, std:0.632404088973999
layer:37, std:0.6271371245384216
layer:38, std:0.6303150653839111
layer:39, std:0.6290847659111023
layer:40, std:0.6289985775947571
layer:41, std:0.621789813041687
layer:42, std:0.625396192073822
layer:43, std:0.6222016215324402
layer:44, std:0.6240432262420654
layer:45, std:0.6275975108146667
layer:46, std:0.6364040374755859
layer:47, std:0.6336819529533386
layer:48, std:0.6304349303245544
layer:49, std:0.6382676959037781
layer:50, std:0.6274499893188477
layer:51, std:0.6260620355606079
layer:52, std:0.6253968477249146
layer:53, std:0.6330998539924622
layer:54, std:0.6337630748748779
layer:55, std:0.6381629705429077
layer:56, std:0.6372403502464294
layer:57, std:0.6365635991096497
layer:58, std:0.6321311593055725
layer:59, std:0.6351718902587891
layer:60, std:0.6261962056159973
layer:61, std:0.6266316771507263
layer:62, std:0.6396113038063049
layer:63, std:0.6292709112167358
layer:64, std:0.6222012042999268
layer:65, std:0.6303234696388245
layer:66, std:0.6274740099906921
layer:67, std:0.6251446604728699
layer:68, std:0.6264793872833252
layer:69, std:0.6295577883720398
layer:70, std:0.6249094009399414
layer:71, std:0.6287401914596558
layer:72, std:0.6286113858222961
layer:73, std:0.6284091472625732
layer:74, std:0.6318932771682739
layer:75, std:0.6292228102684021
layer:76, std:0.6299203038215637
layer:77, std:0.6335345506668091
layer:78, std:0.6286757588386536
layer:79, std:0.6277093291282654
layer:80, std:0.620465099811554
layer:81, std:0.6265316009521484
layer:82, std:0.6293043494224548
layer:83, std:0.6340993046760559
layer:84, std:0.630544900894165
layer:85, std:0.6326507925987244
layer:86, std:0.631687343120575
layer:87, std:0.6303809285163879
layer:88, std:0.6315408945083618
layer:89, std:0.635422945022583
layer:90, std:0.6308826208114624
layer:91, std:0.6228996515274048
layer:92, std:0.6288461089134216
layer:93, std:0.6291288733482361
layer:94, std:0.6311470866203308
layer:95, std:0.6264474987983704
layer:96, std:0.6221898198127747
layer:97, std:0.6308965682983398
layer:98, std:0.6236720681190491
layer:99, std:0.6268938779830933
tensor([[-0.8767, -0.6150, -0.8017,  ...,  0.7821,  0.0101,  0.0245],
        [ 0.3151, -0.0019,  0.5734,  ...,  0.2360, -0.9475, -0.7526],
        [ 0.9089,  0.9743, -0.6852,  ...,  0.4285,  0.8907, -0.5447],
        ...,
        [-0.2722,  0.7697,  0.8062,  ..., -0.7473, -0.4889,  0.9546],
        [-0.9516,  0.5446,  0.9693,  ...,  0.0297, -0.3304, -0.6309],
        [-0.8406, -0.2497,  0.2483,  ..., -0.0112, -0.9767, -0.5765]],
       grad_fn=<TanhBackward>)

可以看到，采用Xavier参数初始化方法后，采用tanh激活函数的神经网络每一层参数的标准差都维持在了0.6左右。

通常，我们还可以使用pytorch提供的函数自动为我们提供gain值。

1
nn.init.calculate_gain(nonlinearity, param=None)

主要功能：返回给定非线性函数的建议增益值。数值如下：

nonlinearity gain
Linear / Identity 1
Conv{1,2,3}D 1
Sigmoid 1
Tanh 53\frac{5}{3}
ReLU 2\sqrt{2}
Leaky Relu 21+negative_slope2\sqrt{\frac{2}{1+\text{negative}\_s\text{lope}^2}}

主要参数

  • nonlinearity: 激活函数名称
  • param: 激活函数的参数，如Leaky ReLU的negative_slop

使用如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import os
import torch
import random
import numpy as np
import torch.nn as nn
from tools.common_tools import set_seed

set_seed(1)  # 设置随机种子

class MLP(nn.Module):
    def __init__(self, neural_num, layers):
        super(MLP, self).__init__()
        self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
        self.neural_num = neural_num

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
            x = torch.tanh(x)
            print("layer:{}, std:{}".format(i, x.std()))
            if torch.isnan(x.std()):
                print("output is nan in {} layers".format(i))
                break
        return x

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                a = np.sqrt(6 / (self.neural_num + self.neural_num))
                tanh_gain = nn.init.calculate_gain('tanh') # tanh_gain=1.66
                a *= tanh_gain                
                nn.init.uniform_(m.weight.data, -a, a)

或者我们也可以直接使用Pytorch提供的方法进行Xavier参数初始化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import os
import torch
import random
import numpy as np
import torch.nn as nn
from tools.common_tools import set_seed

set_seed(1)  # 设置随机种子

class MLP(nn.Module):
    def __init__(self, neural_num, layers):
        super(MLP, self).__init__()
        self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
        self.neural_num = neural_num

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
            x = torch.tanh(x)
            print("layer:{}, std:{}".format(i, x.std()))
            if torch.isnan(x.std()):
                print("output is nan in {} layers".format(i))
                break
        return x

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                tanh_gain = nn.init.calculate_gain('tanh')
				nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)

输出结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
layer:0, std:0.7571136355400085
layer:1, std:0.6924336552619934
layer:2, std:0.6677976846694946
layer:3, std:0.6551960110664368
layer:4, std:0.655646800994873
layer:5, std:0.6536089777946472
layer:6, std:0.6500504612922668
layer:7, std:0.6465446949005127
layer:8, std:0.645668625831604
layer:9, std:0.6414617896080017
layer:10, std:0.6423627734184265
layer:11, std:0.6509683728218079
layer:12, std:0.6584846377372742
layer:13, std:0.6530249118804932
layer:14, std:0.6528729796409607
layer:15, std:0.6523412466049194
layer:16, std:0.6534922122955322
layer:17, std:0.6540238261222839
layer:18, std:0.6477402448654175
layer:19, std:0.6469652652740479
layer:20, std:0.6441705822944641
layer:21, std:0.6484488248825073
layer:22, std:0.6512865424156189
layer:23, std:0.6525684595108032
layer:24, std:0.6531476378440857
layer:25, std:0.6488809585571289
layer:26, std:0.6533839702606201
layer:27, std:0.6482064723968506
layer:28, std:0.6471589803695679
layer:29, std:0.6553042531013489
layer:30, std:0.6560811400413513
layer:31, std:0.6522760987281799
layer:32, std:0.6499099135398865
layer:33, std:0.6568747162818909
layer:34, std:0.6544532775878906
layer:35, std:0.6535675525665283
layer:36, std:0.6508696675300598
layer:37, std:0.6428772807121277
layer:38, std:0.6495102047920227
layer:39, std:0.6479291319847107
layer:40, std:0.6470605731010437
layer:41, std:0.6513484120368958
layer:42, std:0.6503545045852661
layer:43, std:0.6458993554115295
layer:44, std:0.6517390012741089
layer:45, std:0.6520008444786072
layer:46, std:0.6539941430091858
layer:47, std:0.6537034511566162
layer:48, std:0.651664137840271
layer:49, std:0.6535553932189941
layer:50, std:0.6464875936508179
layer:51, std:0.6491114497184753
layer:52, std:0.6455201506614685
layer:53, std:0.65202397108078
layer:54, std:0.6531858444213867
layer:55, std:0.6627185344696045
layer:56, std:0.6544178128242493
layer:57, std:0.6501754522323608
layer:58, std:0.6510435938835144
layer:59, std:0.6549468040466309
layer:60, std:0.6529961824417114
layer:61, std:0.6515753865242004
layer:62, std:0.6453633308410645
layer:63, std:0.6447920799255371
layer:64, std:0.6489525437355042
layer:65, std:0.6553934216499329
layer:66, std:0.6535244584083557
layer:67, std:0.6528763771057129
layer:68, std:0.6492756605148315
layer:69, std:0.6596540808677673
layer:70, std:0.6536692380905151
layer:71, std:0.6498777270317078
layer:72, std:0.6538715362548828
layer:73, std:0.6459632515907288
layer:74, std:0.6543327569961548
layer:75, std:0.6525865197181702
layer:76, std:0.6462062001228333
layer:77, std:0.6534916758537292
layer:78, std:0.6461915969848633
layer:79, std:0.6457912921905518
layer:80, std:0.6481336355209351
layer:81, std:0.649639904499054
layer:82, std:0.6517052054405212
layer:83, std:0.6485037207603455
layer:84, std:0.6395189762115479
layer:85, std:0.6498353481292725
layer:86, std:0.651058554649353
layer:87, std:0.6505323052406311
layer:88, std:0.6573923230171204
layer:89, std:0.6529804468154907
layer:90, std:0.6536460518836975
layer:91, std:0.6497945785522461
layer:92, std:0.6458892226219177
layer:93, std:0.6458885669708252
layer:94, std:0.6530362963676453
layer:95, std:0.6515855193138123
layer:96, std:0.643466055393219
layer:97, std:0.6426210403442383
layer:98, std:0.6407480835914612
layer:99, std:0.6442216038703918
tensor([[ 0.1159,  0.1230,  0.8216,  ...,  0.9417, -0.6332,  0.5106],
        [-0.9586, -0.2355,  0.8550,  ..., -0.2347,  0.9330,  0.0114],
        [ 0.9488, -0.2261,  0.8736,  ..., -0.9594,  0.7923,  0.6266],
        ...,
        [ 0.7160,  0.0916, -0.4326,  ..., -0.9586,  0.2504,  0.5406],
        [-0.9539,  0.5055, -0.8024,  ..., -0.4472, -0.6167,  0.9665],
        [ 0.6117,  0.3952,  0.1042,  ...,  0.3919, -0.5273,  0.0751]],
       grad_fn=<TanhBackward>)

2.2 Kaiming方法

在论文[2]中，提出了一种参数初始化的方法，适用于非饱和激活函数：ReLU及其变种（如Leaky ReLU，PReLU，RReLU）

image-20200801225739149

对于ReLU：D(W)=2ni\mathbf{D}(W)=\frac{2}{n_{i}}，std⁡(W)=2ni\operatorname{std}(W)=\sqrt{\frac{2}{n_{i}}}

发现了吗？由于ReLU这种函数只有正半轴，相比于tanh这种饱和对称函数，方差就要减半。

对于ReLU的变种：D(W)=2(1+a2)⋅ni\mathrm{D}(W)=\frac{2}{\left(1+\mathrm{a}^{2}\right) \cdot n_{i}}，std⁡(W)=2(1+a2)∗ni\operatorname{std}(W)=\sqrt{\frac{2}{\left(1+a^{2}\right) * n_{i}}}

其中a为负半轴的斜率

并且采用0均值的正态分布（均匀分布也行）

使用Kaiming方法初始化的代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import os
import torch
import random
import numpy as np
import torch.nn as nn
from tools.common_tools import set_seed

set_seed(1)  # 设置随机种子

class MLP(nn.Module):
    def __init__(self, neural_num, layers):
        super(MLP, self).__init__()
        self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
        self.neural_num = neural_num

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
            x = torch.relu(x)
            print("layer:{}, std:{}".format(i, x.std()))
            if torch.isnan(x.std()):
                print("output is nan in {} layers".format(i))
                break
        return x

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
				nn.init.normal_(m.weight.data, std=np.sqrt(2 / self.neural_num))

输出结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
layer:0, std:0.826629638671875
layer:1, std:0.8786815404891968
layer:2, std:0.9134422540664673
layer:3, std:0.8892471194267273
layer:4, std:0.834428071975708
layer:5, std:0.874537467956543
layer:6, std:0.7926971316337585
layer:7, std:0.7806458473205566
layer:8, std:0.8684563636779785
layer:9, std:0.9434137344360352
layer:10, std:0.964215874671936
layer:11, std:0.8896796107292175
layer:12, std:0.8287257552146912
layer:13, std:0.8519769906997681
layer:14, std:0.8354345560073853
layer:15, std:0.802306056022644
layer:16, std:0.8613607287406921
layer:17, std:0.7583686709403992
layer:18, std:0.8120225071907043
layer:19, std:0.791111171245575
layer:20, std:0.7164372801780701
layer:21, std:0.778393030166626
layer:22, std:0.8672043085098267
layer:23, std:0.874812662601471
layer:24, std:0.9020991325378418
layer:25, std:0.8585715889930725
layer:26, std:0.7824353575706482
layer:27, std:0.7968912720680237
layer:28, std:0.8984369039535522
layer:29, std:0.8704465627670288
layer:30, std:0.9860473275184631
layer:31, std:0.9080777168273926
layer:32, std:0.9140636920928955
layer:33, std:1.009956955909729
layer:34, std:0.9909380674362183
layer:35, std:1.0253208875656128
layer:36, std:0.849043607711792
layer:37, std:0.703953742980957
layer:38, std:0.7186155319213867
layer:39, std:0.7250635027885437
layer:40, std:0.7030817270278931
layer:41, std:0.6325559020042419
layer:42, std:0.6623690724372864
layer:43, std:0.6960875988006592
layer:44, std:0.7140733003616333
layer:45, std:0.632905125617981
layer:46, std:0.6458898186683655
layer:47, std:0.7354375720024109
layer:48, std:0.6710687279701233
layer:49, std:0.6939153671264648
layer:50, std:0.6889258027076721
layer:51, std:0.6331773996353149
layer:52, std:0.6029313206672668
layer:53, std:0.6145528554916382
layer:54, std:0.6636686325073242
layer:55, std:0.7440094947814941
layer:56, std:0.7972175478935242
layer:57, std:0.7606149911880493
layer:58, std:0.696868360042572
layer:59, std:0.7306802272796631
layer:60, std:0.6875627636909485
layer:61, std:0.7171440720558167
layer:62, std:0.7646605372428894
layer:63, std:0.7965086698532104
layer:64, std:0.8833740949630737
layer:65, std:0.8592952489852905
layer:66, std:0.8092936873435974
layer:67, std:0.806481122970581
layer:68, std:0.6792410612106323
layer:69, std:0.6583346128463745
layer:70, std:0.5702278017997742
layer:71, std:0.5084435939788818
layer:72, std:0.4869326055049896
layer:73, std:0.46350404620170593
layer:74, std:0.4796811640262604
layer:75, std:0.47372108697891235
layer:76, std:0.45414549112319946
layer:77, std:0.4971912205219269
layer:78, std:0.492794930934906
layer:79, std:0.4422350823879242
layer:80, std:0.4802998900413513
layer:81, std:0.5579248666763306
layer:82, std:0.5283755660057068
layer:83, std:0.5451980829238892
layer:84, std:0.6203726530075073
layer:85, std:0.6571893095970154
layer:86, std:0.703682005405426
layer:87, std:0.7321067452430725
layer:88, std:0.6924356818199158
layer:89, std:0.6652532815933228
layer:90, std:0.6728308796882629
layer:91, std:0.6606621742248535
layer:92, std:0.6094604730606079
layer:93, std:0.6019102334976196
layer:94, std:0.595421552658081
layer:95, std:0.6624555587768555
layer:96, std:0.6377885341644287
layer:97, std:0.6079285740852356
layer:98, std:0.6579315066337585
layer:99, std:0.6668476462364197
tensor([[0.0000, 1.3437, 0.0000,  ..., 0.0000, 0.6444, 1.1867],
        [0.0000, 0.9757, 0.0000,  ..., 0.0000, 0.4645, 0.8594],
        [0.0000, 1.0023, 0.0000,  ..., 0.0000, 0.5148, 0.9196],
        ...,
        [0.0000, 1.2873, 0.0000,  ..., 0.0000, 0.6454, 1.1411],
        [0.0000, 1.3589, 0.0000,  ..., 0.0000, 0.6749, 1.2438],
        [0.0000, 1.1807, 0.0000,  ..., 0.0000, 0.5668, 1.0600]],
       grad_fn=<ReluBackward0>)

同样我们可以使用Pytorch提供的Kaiming初始化方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import os
import torch
import random
import numpy as np
import torch.nn as nn
from tools.common_tools import set_seed

set_seed(1)  # 设置随机种子

class MLP(nn.Module):
    def __init__(self, neural_num, layers):
        super(MLP, self).__init__()
        self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
        self.neural_num = neural_num

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
            x = torch.relu(x)
            print("layer:{}, std:{}".format(i, x.std()))
            if torch.isnan(x.std()):
                print("output is nan in {} layers".format(i))
                break
        return x

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
				nn.init.kaiming_normal_(m.weight.data)

输出结果也是相同的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
layer:0, std:0.826629638671875
layer:1, std:0.8786815404891968
layer:2, std:0.9134422540664673
layer:3, std:0.8892471194267273
layer:4, std:0.834428071975708
layer:5, std:0.874537467956543
layer:6, std:0.7926971316337585
layer:7, std:0.7806458473205566
layer:8, std:0.8684563636779785
layer:9, std:0.9434137344360352
layer:10, std:0.964215874671936
layer:11, std:0.8896796107292175
layer:12, std:0.8287257552146912
layer:13, std:0.8519769906997681
layer:14, std:0.8354345560073853
layer:15, std:0.802306056022644
layer:16, std:0.8613607287406921
layer:17, std:0.7583686709403992
layer:18, std:0.8120225071907043
layer:19, std:0.791111171245575
layer:20, std:0.7164372801780701
layer:21, std:0.778393030166626
layer:22, std:0.8672043085098267
layer:23, std:0.874812662601471
layer:24, std:0.9020991325378418
layer:25, std:0.8585715889930725
layer:26, std:0.7824353575706482
layer:27, std:0.7968912720680237
layer:28, std:0.8984369039535522
layer:29, std:0.8704465627670288
layer:30, std:0.9860473275184631
layer:31, std:0.9080777168273926
layer:32, std:0.9140636920928955
layer:33, std:1.009956955909729
layer:34, std:0.9909380674362183
layer:35, std:1.0253208875656128
layer:36, std:0.849043607711792
layer:37, std:0.703953742980957
layer:38, std:0.7186155319213867
layer:39, std:0.7250635027885437
layer:40, std:0.7030817270278931
layer:41, std:0.6325559020042419
layer:42, std:0.6623690724372864
layer:43, std:0.6960875988006592
layer:44, std:0.7140733003616333
layer:45, std:0.632905125617981
layer:46, std:0.6458898186683655
layer:47, std:0.7354375720024109
layer:48, std:0.6710687279701233
layer:49, std:0.6939153671264648
layer:50, std:0.6889258027076721
layer:51, std:0.6331773996353149
layer:52, std:0.6029313206672668
layer:53, std:0.6145528554916382
layer:54, std:0.6636686325073242
layer:55, std:0.7440094947814941
layer:56, std:0.7972175478935242
layer:57, std:0.7606149911880493
layer:58, std:0.696868360042572
layer:59, std:0.7306802272796631
layer:60, std:0.6875627636909485
layer:61, std:0.7171440720558167
layer:62, std:0.7646605372428894
layer:63, std:0.7965086698532104
layer:64, std:0.8833740949630737
layer:65, std:0.8592952489852905
layer:66, std:0.8092936873435974
layer:67, std:0.806481122970581
layer:68, std:0.6792410612106323
layer:69, std:0.6583346128463745
layer:70, std:0.5702278017997742
layer:71, std:0.5084435939788818
layer:72, std:0.4869326055049896
layer:73, std:0.46350404620170593
layer:74, std:0.4796811640262604
layer:75, std:0.47372108697891235
layer:76, std:0.45414549112319946
layer:77, std:0.4971912205219269
layer:78, std:0.492794930934906
layer:79, std:0.4422350823879242
layer:80, std:0.4802998900413513
layer:81, std:0.5579248666763306
layer:82, std:0.5283755660057068
layer:83, std:0.5451980829238892
layer:84, std:0.6203726530075073
layer:85, std:0.6571893095970154
layer:86, std:0.703682005405426
layer:87, std:0.7321067452430725
layer:88, std:0.6924356818199158
layer:89, std:0.6652532815933228
layer:90, std:0.6728308796882629
layer:91, std:0.6606621742248535
layer:92, std:0.6094604730606079
layer:93, std:0.6019102334976196
layer:94, std:0.595421552658081
layer:95, std:0.6624555587768555
layer:96, std:0.6377885341644287
layer:97, std:0.6079285740852356
layer:98, std:0.6579315066337585
layer:99, std:0.6668476462364197
tensor([[0.0000, 1.3437, 0.0000,  ..., 0.0000, 0.6444, 1.1867],
        [0.0000, 0.9757, 0.0000,  ..., 0.0000, 0.4645, 0.8594],
        [0.0000, 1.0023, 0.0000,  ..., 0.0000, 0.5148, 0.9196],
        ...,
        [0.0000, 1.2873, 0.0000,  ..., 0.0000, 0.6454, 1.1411],
        [0.0000, 1.3589, 0.0000,  ..., 0.0000, 0.6749, 1.2438],
        [0.0000, 1.1807, 0.0000,  ..., 0.0000, 0.5668, 1.0600]],
       grad_fn=<ReluBackward0>)

3. 常用初始化方法

十种初始化方法

  1. Xavier均匀分布
  2. Xavier正态分布
  3. Kaiming均匀分布
  4. Kaiming正态分布
  5. 均匀分布
  6. 正态分布
  7. 常数分布
  8. 正交矩阵初始化
  9. 单位矩阵初始化
  10. 稀疏矩阵初始化

参考文献

  1. Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks[C]//Proceedings of the thirteenth international conference on artificial intelligence and statistics. 2010: 249-256. ↩︎

  2. He K, Zhang X, Ren S, et al. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification[C]//Proceedings of the IEEE international conference on computer vision. 2015: 1026-1034. ↩︎