nn网络层-卷积层

发表于 更新于 分类于

1. 1d/2d/3d卷积

卷积维度：一般情况下，卷积核在几个维度上滑动，
就是几维卷积。

image-20200729191742201

2. 卷积-nn.Conv2d

1
2
3
4
5
6
7
8
9
torch.nn.Conv2d(in_channels,
                out_channels,
                kernel_size,
                stride=1,
                padding=0,
                dilation=1,
                groups=1,
                bias=True,
                padding_mode='zeros')

功能：对多个二维信号进行二维卷积

主要参数：

  • in_channels (int) – Number of channels in the input image

  • out_channels (int) – Number of channels produced by the convolution（也即卷积核的数量）

  • kernel_size (int or tuple) – Size of the convolving kernel

  • stride (int or tuple, optional) – Stride of the convolution. Default: 1

  • padding (int or tuple, optional) – Zero-padding added to both sides of the input. Default: 0

  • padding_mode (string*,* optional) – 'zeros', 'reflect', 'replicate' or 'circular'. Default: 'zeros'

  • dilation (int or tuple, optional) – Spacing between kernel elements. Default: 1

  • groups (int, optional) – Number of blocked connections from input channels to output channels. Default: 1

  • bias (bool, optional) – If True, adds a learnable bias to the output. Default: True

kernel_size表示卷积核的尺寸，卷积核越大感受野越大，但是相应计算带复杂度和参数量就会增多。

stride就是卷积的步长，表示每次移动卷积核的长度。步长越大，提取特征越少；反之，提取特征越多。从特征图考虑，stride增大将降低特征图的分辨率。

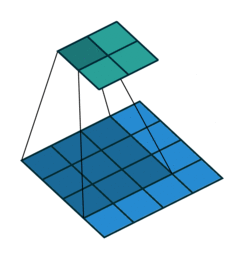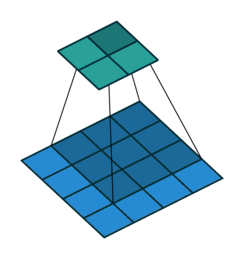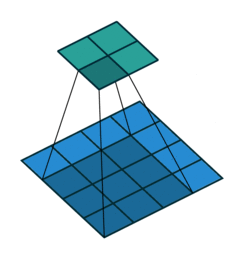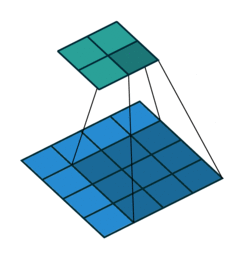
no_padding_no_strides

stride = 1

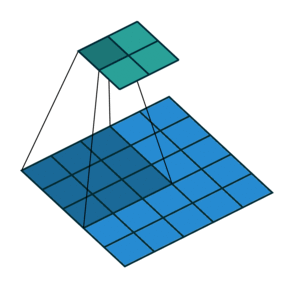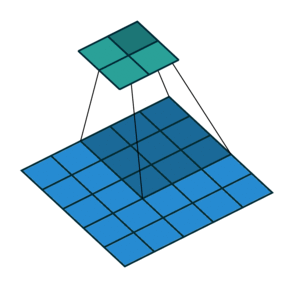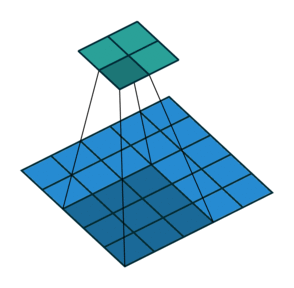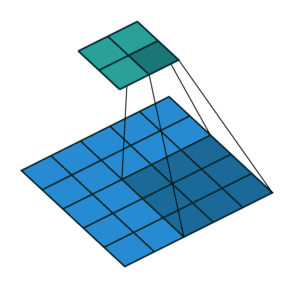
no_padding_strides

stride = 2

padding就是在原图像周围补上一些像素，默认padding=0，即不补值。通过在原图像周围补值可以改变输出的特征图尺寸。

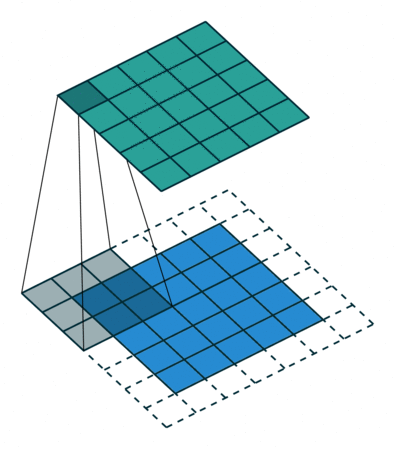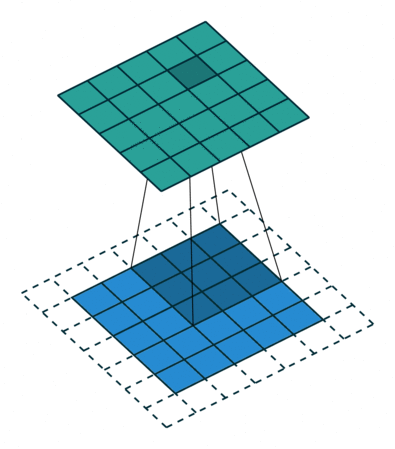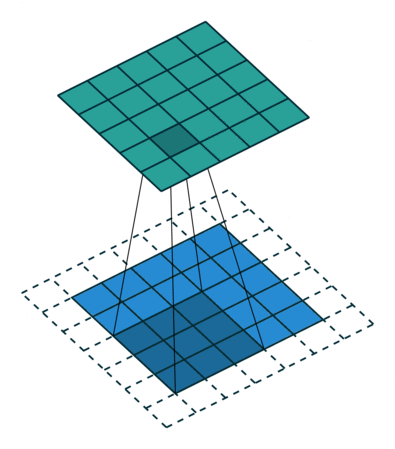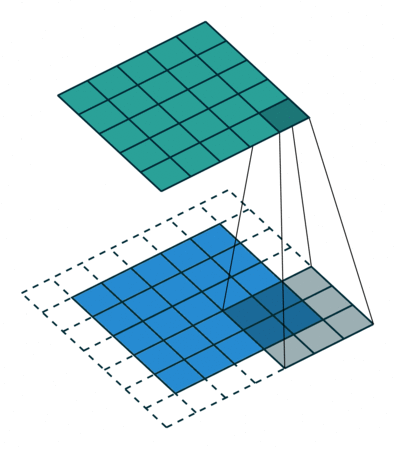
same_padding_no_strides

padding = 1

dilation就是控制卷积核元素之间的距离，默认dilation=1（即普通卷积）。下图是一个3x3的卷积核，dilation=2。较大的dilation可以提高卷积核的感受野。

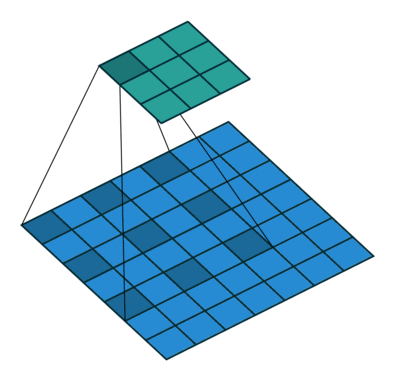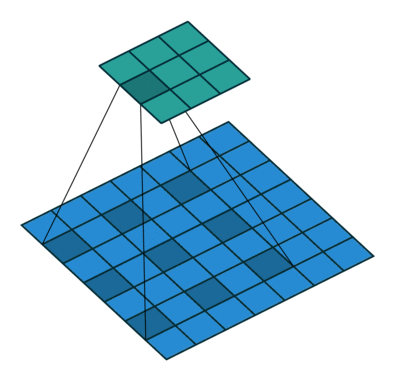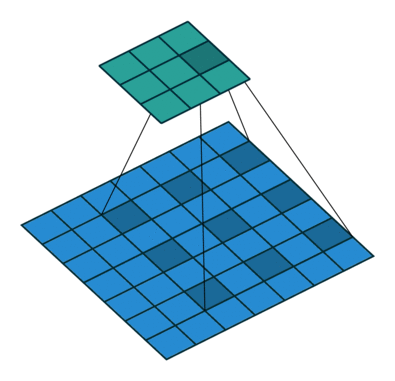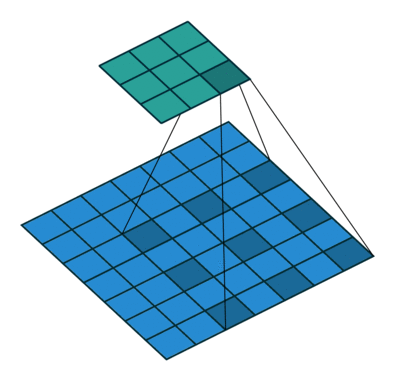
dilation

输出特征图尺寸计算：
简化版：

outsize=Insize−kernelsizestride+1\boldsymbol{o} u t_{s i z e}=\frac{I n_{s i z e}-k e r n e l_{s i z e}}{s t r i d e}+1

完整版：

Hout=⌊Hin+2× padding [0]− dilation [0]×( kernel Size [0]−1)−1 stride [0]+1]H_{\text {out}}=\left\lfloor\frac{H_{\text {in}}+2 \times \text { padding }[0]-\text { dilation }[0] \times\left(\text { kernel }_{\text {Size }}[0]-1\right)-1}{\text { stride }[0]}+1\right]

实验：

主程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import os
import torch.nn as nn
from PIL import Image
from torchvision import transforms
from matplotlib import pyplot as plt
from tools.common_tools import transform_invert, set_seed

set_seed(3)  # 设置随机种子

# =============================== load img ==================================
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "lena.png")
img = Image.open(path_img).convert('RGB')  # 0~255

# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
img_tensor.unsqueeze_(dim=0)    # C*H*W to B*C*H*W

# ========================= create convolution layer =============================
#
#                                  用下面代码填充
#
# =============================== visualization ==================================
print("卷积前尺寸:{}\n卷积后尺寸:{}".format(img_tensor.shape, img_conv.shape))
img_conv = transform_invert(img_conv[0, 0:1, ...], img_transform)
img_raw = transform_invert(img_tensor.squeeze(), img_transform)
plt.subplot(122).imshow(img_conv, cmap='gray')
plt.subplot(121).imshow(img_raw)
plt.show()

  1. 观察stride的影响。

    输入通道为3，输出通道为1（即只有一个卷积核），卷积核尺寸为3x3。

    1
    2
    3
    4
    5
    conv_layer = nn.Conv2d(3, 1, 3)   # input:(i, o, size) weights:(o, i , h, w)
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

    image-20200729205403160

    1
    2
    卷积前尺寸:torch.Size([1, 3, 512, 512])
    卷积后尺寸:torch.Size([1, 1, 510, 510])

    按公式计算：输出的尺寸为(512-3)/1+1 = 510，与实际情况符合。

    将stride改为2，输出特征图尺寸减小。

    1
    2
    3
    4
    5
    conv_layer = nn.Conv2d(3, 1, 3, stride=2)   # input:(i, o, size) weights:(o, i , h, w)
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

    image-20200729210929699

    1
    2
    卷积前尺寸:torch.Size([1, 3, 512, 512])
    卷积后尺寸:torch.Size([1, 1, 255, 255])

    将stride改为3，输出特征图尺寸进一步减小。由于卷积核大小为3x3，所以现在是刚好无重叠也无空隙。

    1
    2
    3
    4
    5
    conv_layer = nn.Conv2d(3, 1, 3, stride=3)   # input:(i, o, size) weights:(o, i , h, w)
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

    image-20200729211219125

    1
    2
    卷积前尺寸:torch.Size([1, 3, 512, 512])
    卷积后尺寸:torch.Size([1, 1, 170, 170])

    进一步增大stride，如下图所示。可以看到，随着stride的加大，特征图的分辨率降低。

    image-20200729211519019

    image-20200729211716550

    image-20200729211755307

    image-20200729211838602

    image-20200729211910516

    stride=20时，特征图分辨率降低到人畜不分了，可爱的lena小姐姐没了。

  2. 观察padding的影响。

    kernel_size=3，padding=1时，输出特征图的尺寸与输入相同。

    1
    2
    3
    4
    5
    conv_layer = nn.Conv2d(3, 1, 3)   # input:(i, o, size) weights:(o, i , h, w)
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

    image-20200729214928974

    1
    2
    卷积前尺寸:torch.Size([1, 3, 512, 512])
    卷积后尺寸:torch.Size([1, 1, 512, 512])

    将padding改成100，由于padding_mode=“zeros”，所以在图像周围填充了宽度为100的一圈0值，卷积以后这些0值还是0，造成输出特征图周围一圈0值。

    image-20200729215635307

    将padding_mode改成reflect，可以看到周围一圈进行了镜像对称。

    1
    2
    3
    4
    5
    conv_layer = nn.Conv2d(3, 1, 3, stride=1, padding=100, padding_mode='reflect')   # input:(i, o, size) weights:(o, i , h, w)
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

    image-20200729215845123

    将padding_mode改成replicate，可以看到周围一圈复制边缘值填充。

    1
    2
    3
    4
    5
    conv_layer = nn.Conv2d(3, 1, 3, stride=1, padding=100, padding_mode='replicate')   # input:(i, o, size) weights:(o, i , h, w)
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

    image-20200729220507733

    将padding_mode改成circular，可以看到周围一圈进行了周期对称。

    1
    2
    3
    4
    5
    conv_layer = nn.Conv2d(3, 1, 3, stride=1, padding=100, padding_mode='circular')   # input:(i, o, size) weights:(o, i , h, w)
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

    image-20200729220906775

    将padding改为512，还是用padding_mode=‘circular’，

    1
    2
    3
    4
    5
    conv_layer = nn.Conv2d(3, 1, 3, stride=1, padding=100, padding_mode='circular')   # input:(i, o, size) weights:(o, i , h, w)
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

    image-20200729221131206

  3. 观察dilation的影响。

    dilation=1就是原图像。

    1
    2
    3
    4
    5
    conv_layer = nn.Conv2d(3, 1, 3, stride=1, dilation=1)   # input:(i, o, size) weights:(o, i , h, w)
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

    image-20200729221703471

    设置dilation逐步增加，观察dilation增加对特征图的影响。

    image-20200729222112682

    image-20200729222724956

    image-20200729222801504

    image-20200729222854585

    image-20200729223102227

    image-20200729223216906

    image-20200729223320923

随着dilation的增加，出现了散光的感觉，这是可以预见的。因为dilation增加会扩大感受野，那么特征图的每一点都会从更大的范围去计算，造成了散光现象。

3. 转置卷积-nn.ConvTranspose

转置卷积又称为反卷积(Deconvolution)和部分跨越卷积(Fractionally-strided Convolution) ，用于对图像进行上采样(UpSample) 。

1
2
3
4
5
6
7
8
9
10
nn.ConvTranspose2d(in_channels, 
                   out_channels,
                   kernel_size, 
                   stride=1,
                   padding=0, 
                   output_padding=0, 
                   groups=1,
                   bias=True, 
                   dilation=1, 
                   padding_mode='zeros')

主要参数：

  • stride controls the stride for the cross-correlation.
  • padding controls the amount of implicit zero-paddings on both sides for dilation * (kernel_size - 1) - padding number of points. See note below for details.
  • output_padding controls the additional size added to one side of the output shape. See note below for details.
  • dilation controls the spacing between the kernel points; also known as the à trous algorithm. It is harder to describe, but this link has a nice visualization of what dilation does.
  • groups controls the connections between inputs and outputs. in_channels and out_channels must both be divisible by groups.

ConvTranspose2d的参数设置是为了去抵消Conv2d造成的影响，所以这里的stride不是正常意义的步长，而是为了抵消在Conv2d中stride参数造成的影响，其他参数同理。

实验：

  1. 观察stride的影响。

    输入通道为3，输出通道为1（即只有一个卷积核），卷积核尺寸为3x3。

    1
    2
    3
    4
    5
    conv_layer = nn.ConvTranspose2d(3, 1, 3, stride=1)   # input:(i, o, size)
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

    image-20200730122335305

    1
    2
    卷积前尺寸:torch.Size([1, 3, 512, 512])
    卷积后尺寸:torch.Size([1, 1, 514, 514])
    no_padding_no_strides_transposed

    可以看到，转置卷积会自动在输入图像周围补零，即使stride=1，输出特征图也会比输入图像要大。

    若在输入图像周围补上kernel_size-1的一圈0，并把卷积核上下左右翻转，那么nn.Conv2d和nn.ConvTranspose的输出是相同的

    对比stride=1的Conv2d，可以看到他们从“形式上”互为逆运算（其实卷积是不可逆的，因为真正的逆运算必须使用IIR的滤波器，那么就变得不可实现了）

    no_padding_no_strides

    下图是先使用nn.Conv2d(3, 1, 3, stride=1)再使用nn.ConvTranspose2d(1, 1, 3, stride=1)的结果。(由于卷积核的参数为随机值，所以重建图像是没有什么具体意义的)

    image-20200730141311447

    1
    2
    卷积前尺寸:torch.Size([1, 3, 512, 512])
    卷积后尺寸:torch.Size([1, 1, 512, 512])

    令stride=2，反卷积的stride其实是在控制输入图像的dilation。下图是stride=2的示意图。

    no_padding_strides_transposed

    输出图像为：

    image-20200730131947701

    对比stride=2的Conv2d，输出特征图一个点和输入的9个点相关。

    no_padding_strides

    对比一下，他们在形式上相逆。

    image-20200730161546882 image-20200730161752746

    下图是先使用nn.Conv2d(3, 1, 3, stride=1)再使用nn.ConvTranspose2d(1, 1, 3, stride=1)的结果。

    image-20200730161949921

    1
    2
    卷积前尺寸:torch.Size([1, 3, 512, 512])
    卷积后尺寸:torch.Size([1, 1, 511, 511])

    进一步增大stride值，先Conv2d再ConvTranspose2d，输出图像如下所示：

    image-20200730132037029

    image-20200730162427091

    image-20200730132113360

    image-20200730162354832

    image-20200730132421032

    image-20200730162306015

    当stride大于kernel_size时，可以预见会有很多卷积核在全0的图像上卷积。并且当stride越大时，重建的质量是变差的。所以在FCN等需要用转置卷积上采样的模型时，应该通过多次的小stride的转置卷积重建图像，这样往往也带来了更大的参数量。

  2. 观察padding的影响。

    1
    2
    3
    4
    5
    conv_layer = nn.ConvTranspose2d(3, 1, 3, stride=1, padding=10)   # input:(i, o, size)
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

    image-20200730164140536

    1
    2
    卷积前尺寸:torch.Size([1, 3, 512, 512])
    卷积后尺寸:torch.Size([1, 1, 494, 494])

    继续增大padding，输出如下所示：

    image-20200730164252835

    1
    2
    卷积前尺寸:torch.Size([1, 3, 512, 512])
    卷积后尺寸:torch.Size([1, 1, 414, 414])

    image-20200730164330162

    1
    2
    卷积前尺寸:torch.Size([1, 3, 512, 512])
    卷积后尺寸:torch.Size([1, 1, 314, 314])

    可以发现，当padding增大时，对原图像的感受区域是在减小的，有放大图片的感觉。这是因为在Conv2d中padding会在输入图像周围扩充一圈0值，ConvTranspose为了抵消这种影响当然是对图像的中间的区域感兴趣，而不关注外面一圈0值（转置卷积的只能应对Conv2d当padding_mode=‘zeros’的情况。换言之，转置卷积的padding_mode参数只能等于’zeros’）

    下图是padding=2的Conv2d，输入图像size为5x5，输出特征图size为6x6.

    arbitrary_padding_no_strides

    下图是padding=2的ConvTranspose，输入图像size为6x6，输出特征图size为5x5.

    arbitrary_padding_no_strides_transposed

    可见，ConvTranspose的padding是根据Conv2d的padding自动计算出的，上图为了使输出恢复到5x5的大小，ConvTranspose在输入周围加了一圈0值。以下是用不同的padding参数先做Conv2d，再做ConvTranspose的结果：

    image-20200730192122152

    image-20200730192155630

    image-20200730192237099

    可以发现，上面三张图没啥区别，说明了padding的恢复应该是无损的。

  3. 观察dilation的影响

    1
    2
    3
    4
    5
    conv_layer = nn.ConvTranspose2d(1, 1, 3, stride=1, dilation=2)   # input:(i, o, size)
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

    image-20200730200743037

    上图是对左边的图像直接做ConvTranspose2d(3, 1, 3, stride=1, dilation=2)的结果，下图是先做Conv2d(3, 1, 3, stride=1, dilation=2)再做ConvTranspose2d(1, 1, 3, stride=1, dilation=2)的结果。

    image-20200730202106747

    下面依次是Conv2d，和先做Conv2d再做ConvTranspose2d重建的结果

    image-20200730200921897

    image-20200730202352933

    image-20200730201004554

    image-20200730202428417

    可以发现ConvTranspose2d对dilation的恢复不是那么好（卷积核权值是随机的，所以可能也说明不了这个问题）

    关于ConvTranspose2d的dilation是怎么实现的没查到资料