nn网络层-池化-线性-激活函数层

1. 池化层——Pooling Layer

池化运算：对信号进行 “收集”并 “总结”。

“收集”：多变少

“总结”：最大值/平均值

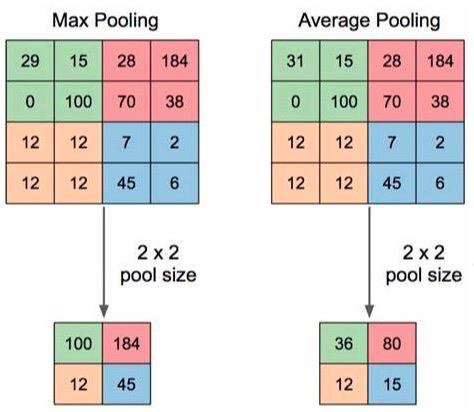
1.1 nn.MaxPool2d

nn.MaxPool2d(kernel_size, 
             stride=None, 
             padding=0, 
             dilation=1, 
             return_indices=False, 
             ceil_mode=False)

功能：对二维信号（图像）进行最大值池化
主要参数：

• kernel_size：池化核尺寸
• stride：步长
• padding ：填充个数
• dilation：池化核间隔大小
• ceil_mode：尺寸向上取整
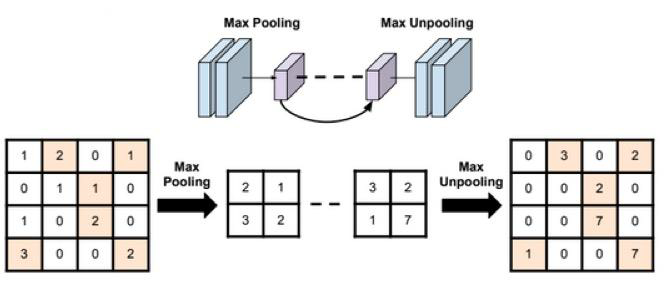
• return_indices：记录池化像素索引（用于反池化时选择位置，如下图所示）

import os
import torch
import random
import numpy as np
import torchvision
import torch.nn as nn
from torchvision import transforms
from matplotlib import pyplot as plt
from PIL import Image
from tools.common_tools import transform_invert, set_seed

set_seed(1)  # 设置随机种子

# ================================= load img ===================================
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "lena.png")
img = Image.open(path_img).convert('RGB')  # 0~255

# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
img_tensor.unsqueeze_(dim=0)    # C*H*W to B*C*H*W

# ============================ create convolution layer =========================
#
#                                  使用下面代码填充
#
# =============================== visualization =================================
print("池化前尺寸:{}\n池化后尺寸:{}".format(img_tensor.shape, img_pool.shape))
img_pool = transform_invert(img_pool[0, 0:3, ...], img_transform)
img_raw = transform_invert(img_tensor.squeeze(), img_transform)
plt.subplot(122).imshow(img_pool)
plt.subplot(121).imshow(img_raw)
plt.show()

1. 观察kernel_size和stride参数。

   用2x2池化并且步长为2，则不重叠刚好4选1。一般来说，池化都是不重叠的，也就是kernel_size = stride。

   maxpool_layer = nn.MaxPool2d(2, stride=2)   # input:(i, o, size) weights:(o, i , h, w)
   img_pool = maxpool_layer(img_tensor)

   

   池化前尺寸:torch.Size([1, 3, 512, 512])
   池化后尺寸:torch.Size([1, 3, 256, 256])

   下图为逐渐增大kernel_size和stride的输出图像。

   

   

   可见，池化就是一个下采样（抽取）的过程。

2. 观察padding参数

   padding必须小于kernel_size的一半，否则就会报错。函数不希望产生池化后是0的值。padding在图像外围最多补一圈kernel_size/2的0值。

   maxpool_layer = nn.MaxPool2d(2, stride=2, padding=1)   # input:(i, o, size) weights:(o, i , h, w)
   img_pool = maxpool_layer(img_tensor)

   

   池化前尺寸:torch.Size([1, 3, 512, 512])
   池化后尺寸:torch.Size([1, 3, 257, 257])

   可以看到，相比padding=0的情况，输出图像的尺寸大了1。

3. 观察dilation参数，dilation的池化不再是连续的方块中取一个最大的了，dilation的池化核和dilation的卷积核是差不多的，卷积核的元素之间有空隙。

   maxpool_layer = nn.MaxPool2d(2, stride=2, dilation=5)   # input:(i, o, size) weights:(o, i , h, w)
   img_pool = maxpool_layer(img_tensor)

   

   池化前尺寸:torch.Size([1, 3, 512, 512])
   池化后尺寸:torch.Size([1, 3, 254, 254])

   可以预见结果，dilation池化也会造成散光的效果。输出特征图的尺寸是不小的，同样输出尺寸下不加dilation肯定不会有一丝模糊。

1.2 nn.AvgPool2d

nn.AvgPool2d(kernel_size, 
             stride=None, 
             padding=0, 
             ceil_mode=False, 
             count_include_pad=True, 
             divisor_override=None)

功能：对二维信号（图像）进行平均值池化
主要参数：

• kernel_size：池化核尺寸
• stride：步长
• padding ：填充个数
• ceil_mode：尺寸向上取整
• count_include_pad：填充值用于计算
• divisor_override ：除法因子（默认是卷积核的大小，如果设置了这个参数则用设置的数做平均的分母）

avgpoollayer = nn.AvgPool2d(2, stride=2)   # input:(i, o, size) weights:(o, i , h, w)
img_pool = avgpoollayer(img_tensor)

比nn.MaxPool2d(2, stride=2)输出的图像亮度会暗一些，毕竟是取了平均的操作。 如果设置divisor_override =1就会亮很多了，同样如果设置divisor_override =8就会暗很多。

当divisor_override 小于kernel_size的时候，求出来的像素值可能会超过量化的最大值，造成类似颜色泄露奇怪的现象（也不知道颜色超过量化最大值PIL包是做削顶还是循环处理）。

kernel_size=2，divisor_override=3时情况会减轻。

avgpoollayer = nn.AvgPool2d(2, stride=2, divisor_override=3)   # input:(i, o, size) weights:(o, i , h, w)
img_pool = avgpoollayer(img_tensor)

kernel_size=3，divisor_override=8时情况会减轻更多。

avgpoollayer = nn.AvgPool2d(3, stride=3, divisor_override=8)   # input:(i, o, size) weights:(o, i , h, w)
img_pool = avgpoollayer(img_tensor)

当divisor_override 大于kernel_size的时候，输出图像的确是变暗的

1.3 nn.MaxUnpool2d

nn.MaxUnpool2d(kernel_size, 
               stride=None, 
               padding=0)

功能：对二维信号（图像）进行最大值池化上采样

主要参数：

• kernel_size：池化核尺寸
• stride：步长
• padding ：填充个数

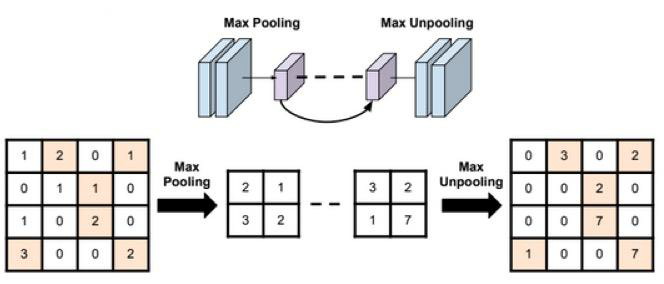
MaxUnpool2d就是把输入的元素放到指定的位置，其他地方填0，如上图所示，需要使用Maxpool2d的indices。

就需要使用Maxpool2d的indices，

# pooling
maxpool_layer = nn.MaxPool2d(2, stride=2, return_indices=True)
img_pool, indices = maxpool_layer(img_tensor)

# unpooling
maxunpool_layer = nn.MaxUnpool2d(2, stride=2)
img_unpool = maxunpool_layer(img_pool, indices)

上面代码截取了原图像RGB通道在2x2池化核中的最大值，并且放回至原来截取的位置得到最右边的图片。（按右图的结果，猜测RGB3个通道的indices是独立的，也就是说在同一块池化核中，三个通道的位置是独立记录的，因此才会造成右图中花花绿绿的情况。）

2. 线性层——Linear Layer

线性层又称全连接层，其每个神经元与上一层所有神经元相连
实现对前一层的线性组合，线性变换。

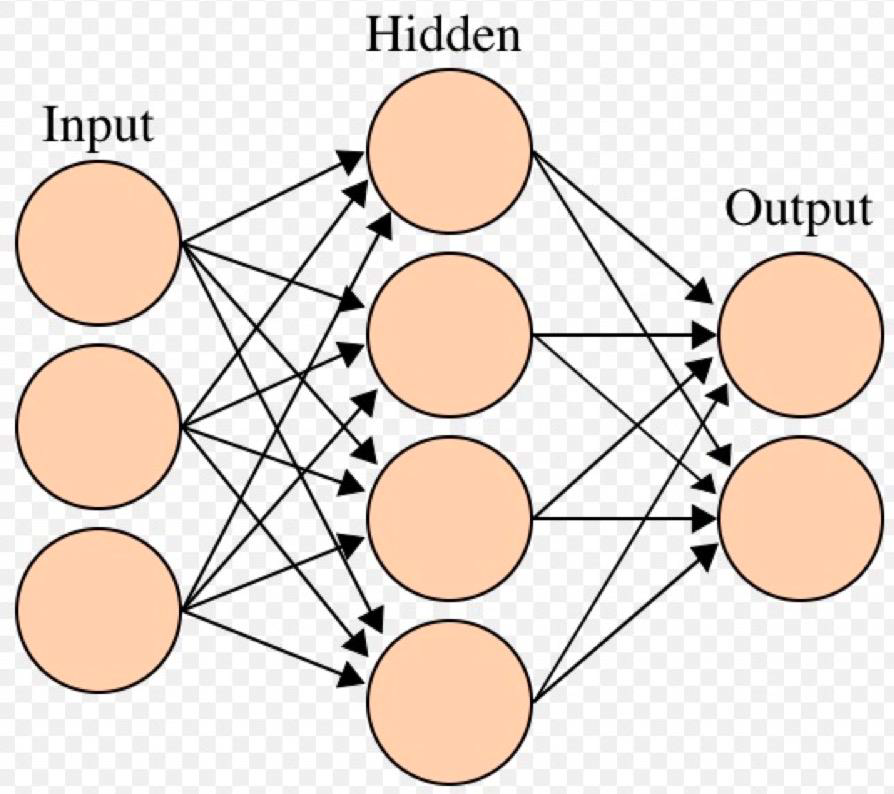
2.1 nn.Linear

nn.Linear(in_features, 
          out_features, 
          bias=True)

功能：对一维信号（向量）进行线性组合 主要参数：
• in_features：输入结点数
• out_features：输出结点数
• bias ：是否需要偏置
计算公式：$y=xW^{T}+bias$

inputs = torch.tensor([[1., 2, 3]])
linear_layer = nn.Linear(3, 4)
linear_layer.weight.data = torch.tensor([[1., 1., 1.],
                                         [2., 2., 2.],
                                         [3., 3., 3.],
                                         [4., 4., 4.]])

linear_layer.bias.data.fill_(0.5)
output = linear_layer(inputs)
print(inputs, inputs.shape)
print(linear_layer.weight.data, linear_layer.weight.data.shape)
print(output, output.shape)

tensor([[1., 2., 3.]]) torch.Size([1, 3])
tensor([[1., 1., 1.],
        [2., 2., 2.],
        [3., 3., 3.],
        [4., 4., 4.]]) torch.Size([4, 3])
tensor([[ 6.5000, 12.5000, 18.5000, 24.5000]], grad_fn=<AddmmBackward>) torch.Size([1, 4])

3. 激活函数层——Activation Layer

3.1 nn.Sigmoid

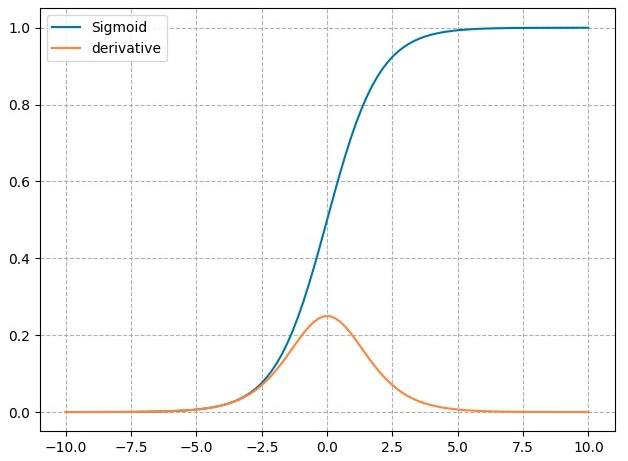
计算公式：$y=\frac{1}{1+e^{-x}}$

梯度公式：𝒚′ = 𝒚 ∗ (1 − 𝒚)

特性：

• 输出值在(0,1)，符合概率
• 导数范围是[0, 0.25],易导致梯度消失
• 输出为非0均值，破坏数据分布

3.2 nn.tanh

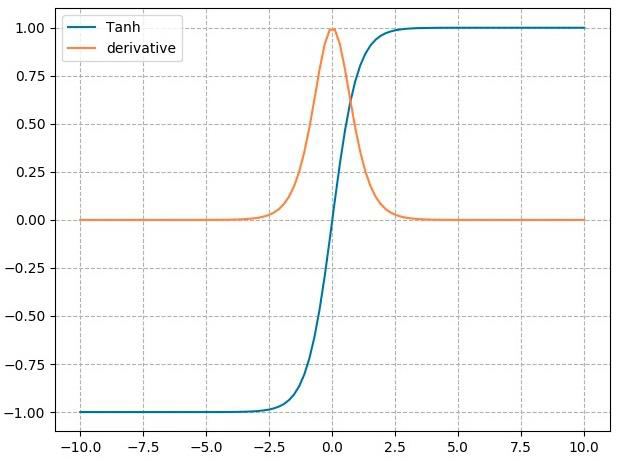
计算公式：$y=\frac{\sin x}{\cos x}=\frac{e^{x}-e^{-x}}{e^{-}+e^{-x}}=\frac{2}{1+e^{-2 x}}+1$

梯度公式：$y^{\prime}=1-y^{2}$

特性：

• 输出值在(-1,1)，数据符合0均值
• 导数范围是(0, 1),易导致梯度消失

3.3 nn.ReLU

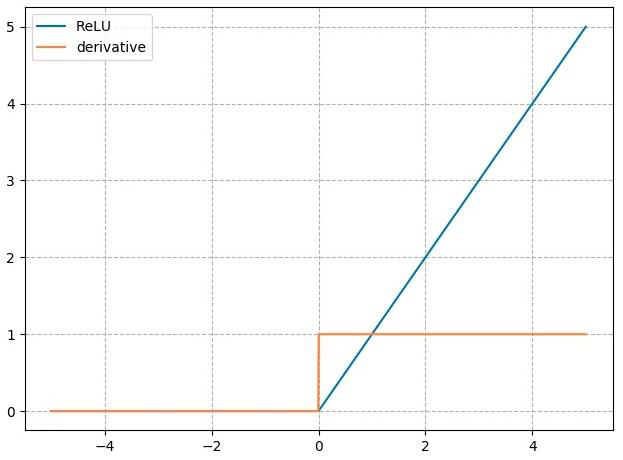
计算公式：$\mathbf{y}=\max (\mathbf{0}, x)$

梯度公式：$y^{\prime}=\left\{\begin{array}{ll}1, & x>0 \\ u n d e f \text { ine } d, & x=0 \\ 0, & x<0\end{array}\right.$

特性：

• 输出值均为正数，负半轴导致死神经元
• 导数是1,缓解梯度消失

3.4 改进型ReLU

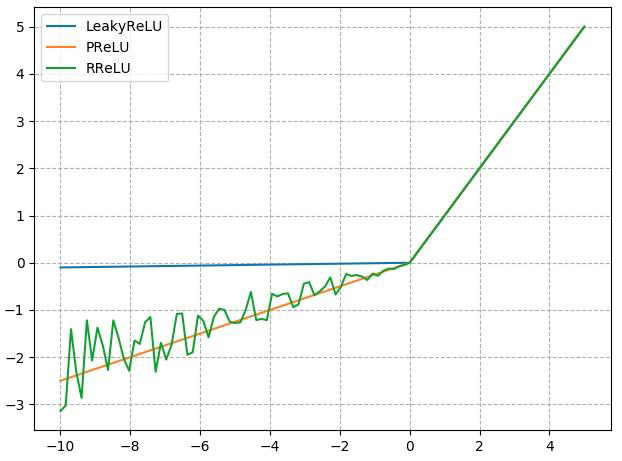
3.4.1 nn.LeakyReLU

• negative_slope: 负半轴斜率

3.4.2 nn.PReLU

• init: 可学习斜率

3.4.3 nn.RReLU

• lower: 均匀分布下限
• upper:均匀分布上限